The FFORMPP paper is accepted in the International Journal of Forecasting
Thiyanga S. Talagala, Feng Li, Yanfei Kang (2021). FFORMPP: Feature-based forecast model performance prediction. International Journal of Forecasting. (in press)
This paper introduces a novel meta-learning algorithm for time series forecast model performance prediction. We model the forecast error as a function of time series features calculated from the historical time series with an efficient Bayesian multivariate surface regression approach. The minimum predicted forecast error is then used to identify an individual model or a combination of models to produce the final forecasts. It is well-known that the performance of most meta-learning models depends on the representativeness of the reference dataset used for training. In such circumstances, we augment the reference dataset with a feature-based time series simulation approach, namely GRATIS, in generating a rich and representative time series collection. The proposed framework is tested using the M4 competition data and is compared against commonly used forecasting approaches. Our approach provides comparable performances to other model selection/combination approaches but at a lower computational cost and a higher degree of interpretability, which is important for supporting decisions. We also provide useful insights regarding which forecasting models are expected to work better for particular types of time series, the intrinsic mechanisms of the meta-learners and how the forecasting performances are affected by various factors.
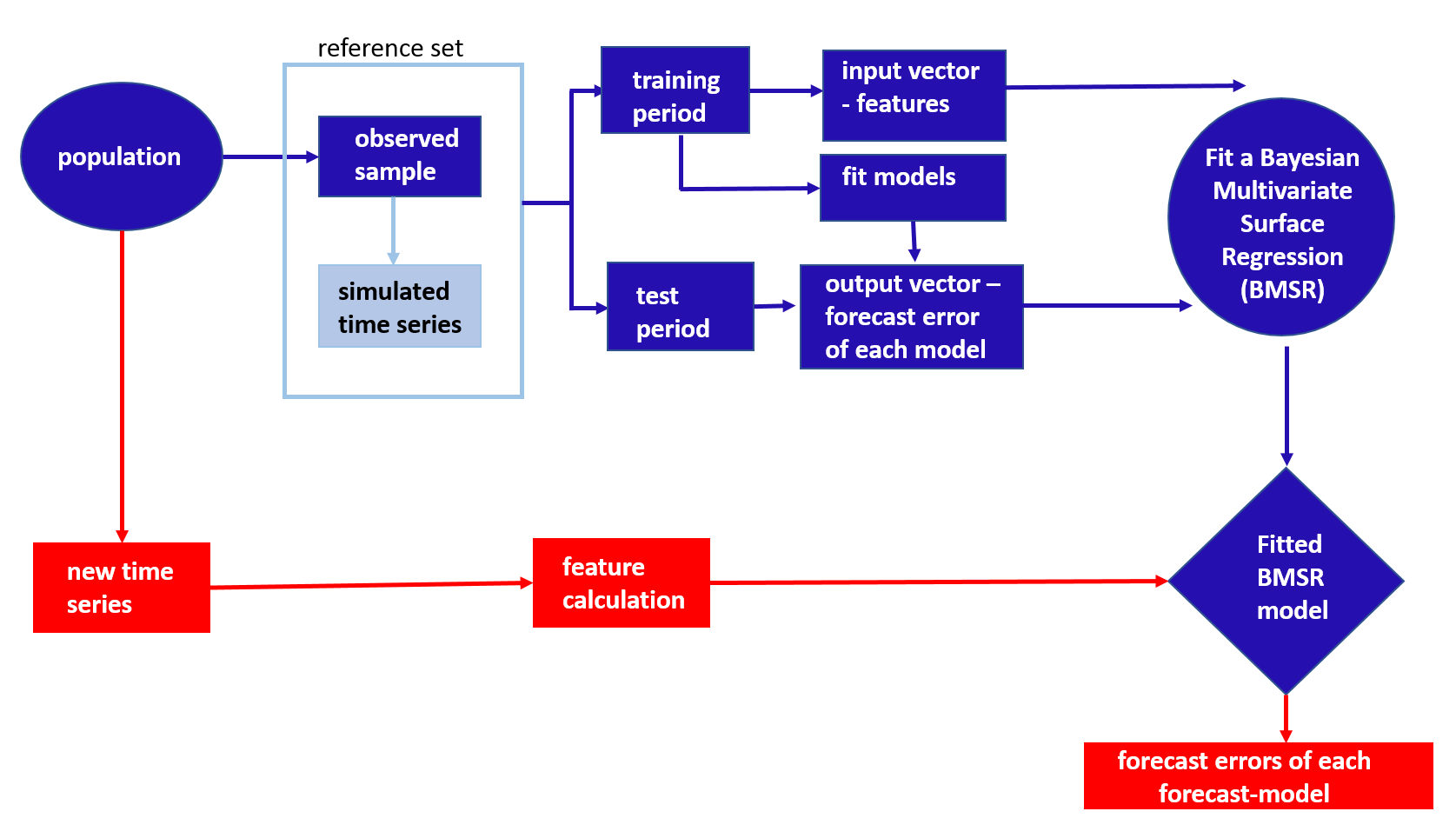
Our first attempt to develop a framework for forecast model selection is described in Talagala, Hyndman & Athanasopoulos (2018). The first framework is called FFORMS: Feature-based FORecast Model-Selection, in which we use a classification algorithm (random forest) to predict the “best forecast model” on a given time series. Our following-up essay, Montero-Manso et al. (2020), rather than mapping time series to a single forecast model, uses a gradient boosting algorithm to obtain the weights for forecast combinations. The second framework is named FFORMA: Feature-based FORecast Model Averaging. FFORMA placed second in the M4 competition (Makridakis, Spiliotis & Assimakopoulos, 2018). This paper, which is the third in this series, considered the correlation structure of algorithm performance in their model training process. Having revisited the literature, we found that, to the best of our knowledge, few of these studies have tackled the forecast model performance prediction with meta-learning. In a conventional univariate supervised meta-learning problem, merely labelling the instances using the “best forecast model” is difficult for the meta- learner to correctly retrieve the interconnections between individual forecast models. The current paper further extends the idea of meta-learning by making the dependent variables a multivariate forecast errors vector. Hence, the meta-model is trained to learn the interrelationship between
the forecast errors across different class labels.
Our results show that features of time series are useful in selecting an optimal subset of models from all individual models without the need to run all possible combinations of individual models during the online phase. Apart from the obvious utility of this approach for forecast model selection, the ranking of models provides an alternative solution to practitioners who may wish to incorporate their own judgements or expertise into the forecasting decision process. We further explored the instance space defined by features to understand how certain features of the time series are influencing the forecast model selection. A further contribution of the paper is the provision of empirical support for the findings of the M4 competition (Makridakis, Spiliotis & Assimakopoulos, 2018) that hold that the combination forecasts, in general, outperform the best individual forecasts. An interesting future extension of this framework would be to apply this methodology to produce probabilistic forecasts.
Leave a Reply